循环神经网络

对于图像数据，我们设计了专门的卷积神经网络架构来为这类特殊的数据结构建模；而对于序列输入，用循环神经网络则能够更好地处理；

其中序列被定义为一串在时间上有序的数据，并且这些数据背后的动力学规律不随时间改变

序列模型

序列模型

用 $x_t$ 表示在时间步 $t$ 时的目标函数值。请注意， $t$ 对于本文中的序列通常是离散的，并在整数或其子集上变化。形式上序列建模就是对下面的概率分布函数建模：

$$x_t\sim P(x_t|x_{t-1},x_{t-2},...,x_1)$$

考虑到动力学规律的不变性，整个序列的概率估计为

$$P(x_1,...,x_T)=\prod _{t=1}^{T}P(x_t|x_{t-1},x_{t-2},...,x_1)$$

然而需要处理的数据会随着时间累积，我们需要对于这样的变化进行处理。有两种常用方法可以处理：1️⃣只利用长度为 $\tau$ 的序列信息；2️⃣将之前所有的序列信息压缩进入一个隐藏变量 $h_t$ ，每个时间步都会预测目标函数以及更新 $h_t$ ；

其中第一种叫做自回归模型，第二种叫做隐变量自回归模型

相关术语

如果已经观测到的数据到了 $x_t$ 那么在时间步 $t+k$ 处的预测输出 ${\hat{x}}_{t+k}$ 被称作“$k$ 步预测”；由于多步预测过程中，误差会逐步累积，因此多步预测有时很困难

这张图是在简单的多层感知机的基础上训练的，用于拟合含有高斯噪声的正弦时间序列

指向原始笔记的链接

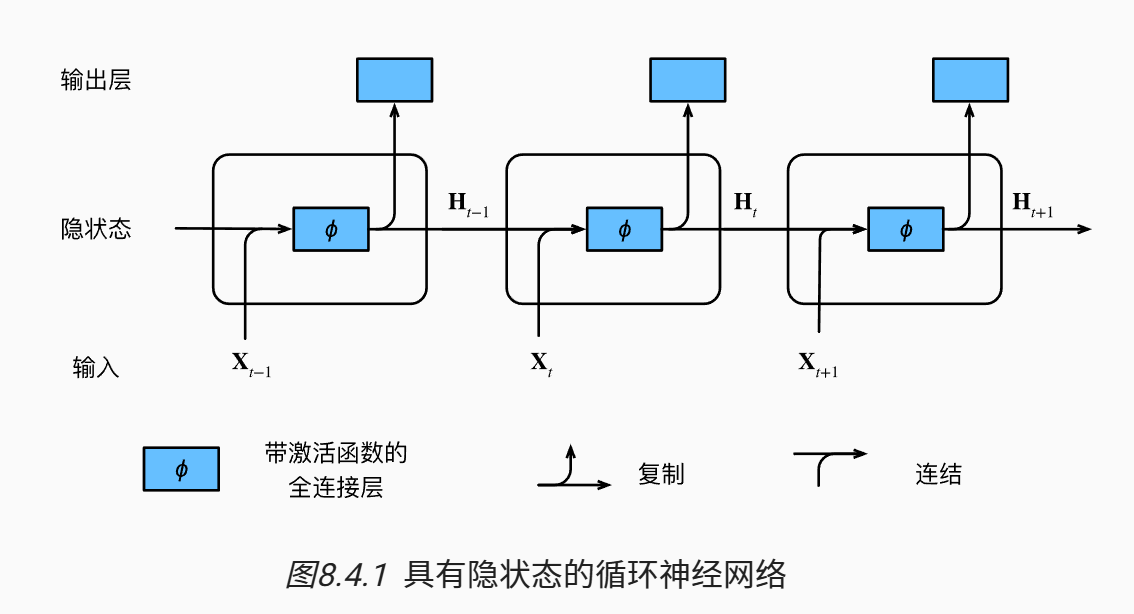
循环神经网络简单架构

循环神经网络架构的核心就是引入了一个固定长度的隐变量 $H_t$ ；当前时间步隐藏变量由当前时间步的输入与前一个时间步的隐藏变量一起计算得出：

$$H_t=\varphi (X_t{W}_{xh}+H_{t-1}{W}_{hh}+b_h).$$

$H_t,H_{t-1},\dots$ 这些变量捕获并保留了序列直到其当前时间步的历史信息，就如当前时间步下神经网络的状态或记忆，因此这样的隐藏变量被称为隐状态(hidden state)；由于每一个时间步中，隐状态使用的定义与前一个时间步中使用的定义相同，因此我们称上面这个式子的计算是循环的(recurrent)；执行上面这个式子所表示的计算的神经网络层被称为循环层(recurrent layer)；

计算技巧

$X_t{W}_{xh}+H_{t-1}{W}_{hh}$ 对应的计算相当于 $X_t$ 和 $H_{t-1}$ 的拼接与 $W_{xh}$ 和 $W_{hh}$ 的拼接的矩阵乘法；注意拼接方向不同

困惑度

困惑度

困惑度，Perplexity，一个用于度量语言模型生成的语言质量的标量指标；本质上是完全随机分布与模型表示的条件分布的交叉熵；

从信息论的角度来说，一个更好的语言模型应该能让我们更准确地预测下一个词元；换言之，它应该允许我们在压缩序列时花费更少的比特。

由于完全随机分布理论上存储的比特数最少，所以我们通过 n 个词元的完全随机分布和我们模型对应的条件概率分布之间的交叉熵来衡量模型相较于完全随机分布需要的比特数：

$$\sum _{t=1}^n-\frac{1}{n}\log P(x_t|x_{t-1},\dots ,x_1)$$

而更进一步，困惑度就是上述交叉熵的指数：

$$Perplexity=\exp \left\{\sum _{t=1}^n-\frac{1}{n}\log P(x_t|x_{t-1},\dots ,x_1)\right\}$$指向原始笔记的链接

梯度截断

梯度截断

在 RNN 中，过长的序列可能会导致梯度消失或者梯度爆炸；一个朴素的思想就是避免完全计算所有的矩阵乘法链来得到最终的梯度，我们可以进行截断，在计算一定长度的反向传播链之后将得到的结果作为最终结果的近似；

定长截断

如题，在计算某个恒定步长的反向传播之后截断；

随机截断

通过某些数学操作能够实现随机截断的效果；但是在实际应用过程中，与定长截断相比没有突出的优势，其原因如下：

1. 经过随机步数的反向传播，模型难以正确捕获依赖关系
2. 按道理来说有一些更长的反向传播步数会得到更加精确的结果，但是随机的截断步数引起了结果更大的方差，导致结果并没有预期中那么稳定
3. 在实际生成过程中，我们也更倾向于使用更短的时间步来进行预测；因为预测过长的时间步总是会得到更差的效果，这是无法避免的

定长截断评述

定长截断其实也发挥了一个“轻微正则化”的效果，能够让模型避免过长的依赖关系；这样做是基于“模型不会依赖太长的输入”这个经验性的假设；

指向原始笔记的链接

现代循环神经网络

循环神经网络实践中经常出现的缺陷就是数值不稳定，并且我们在实际应用过程中常常需要更多的控制：1️⃣让模型能够跳过某些无关信息或者增强某些关键信息；2️⃣序列可能存在中断的情况，需要进行内部状态的重置；

门控循环单元(GRU)

门控循环单元(Gated Recurrent Unit)赋予了模型更高阶的控制隐状态的能力，模型将能够学习 1️⃣何时忽略或者增强某个信息；2️⃣模型将能够学习何时重置内部隐状态；

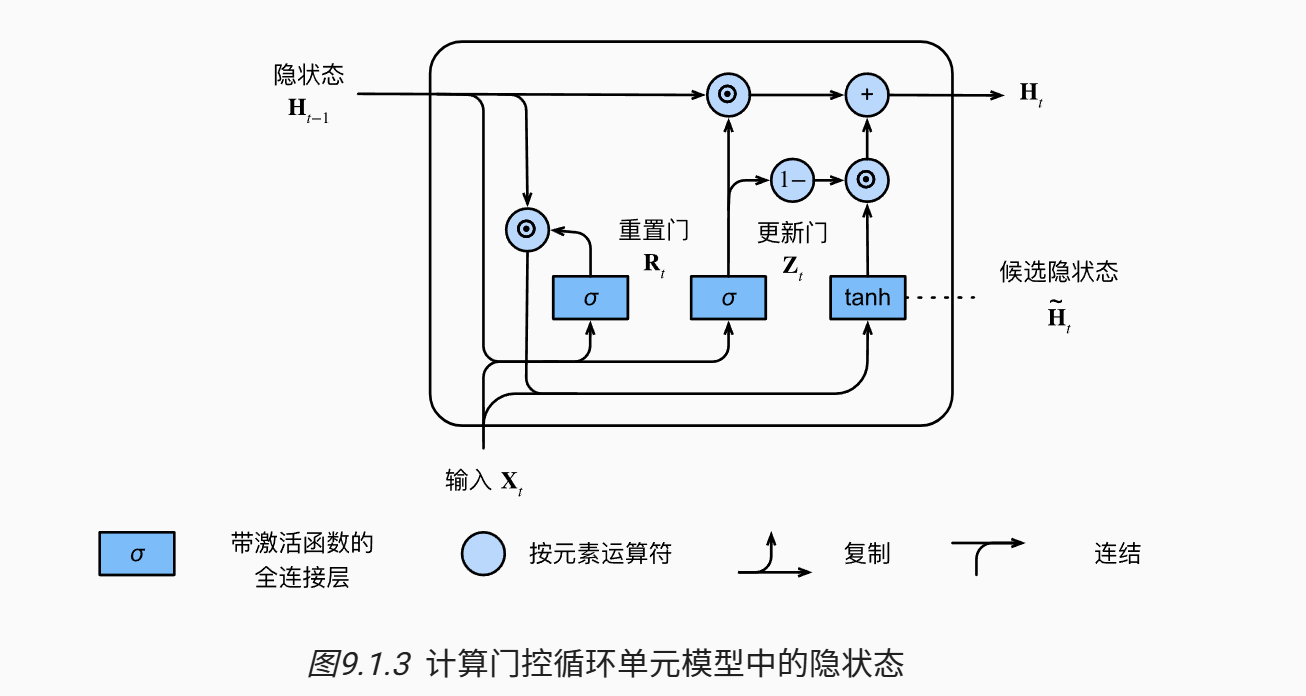
主要由重置门和更新门组成，都是一组可学习的向量；重置门的计算结果 $R_t$ 和更新门的计算结果 $Z_t$ 如下：

$$R_t=\sigma (X_t{W}_{xr}+H_{t-1}{W}_{hr}+b_r)$$ $$Z_t=\sigma (X_t{W}_{xz}+H_{t-1}{W}_{hz}+b_z)$$

当 $R_t$ 中的项接近 0 时，隐状态 $H_{t-1}$ 的影响将被擦除； 候选隐状态 ${\tilde{H}}_t$ 计算如下：

$${\tilde{H}}_t=\tanh (X_t{W}_{xh}+(R_t\odot H_{t-1})W_{hh}+b_h)$$

通过一个凸组合来引入更新门的效果，得到新的隐状态：

$$H_t=Z_t\odot H_{t-1}+(1-Z_t)\odot {\tilde{H}}_t$$

当 $Z_t$ 接近 1 时，模型倾向于保留旧有状态；

长短期记忆网络

长短期记忆网络(LSTM)